どうも。おいちゃんによる標準偏差についての独習です。テキストには載っていないのですが、以前統計計算の復習をしたときに確認した内容です。
データのばらつきはどちらが大きい?
以下ふたつのデータの比較をしてみます。
\begin{eqnarray}
\{A_{n}\}&=&6, 3, 3, 7, 6\\
\{B_{n}\}&=&4.8, 5.3, 5.4, 4.8, 4.7
\end{eqnarray}
\{A_{n}\}&=&6, 3, 3, 7, 6\\
\{B_{n}\}&=&4.8, 5.3, 5.4, 4.8, 4.7
\end{eqnarray}
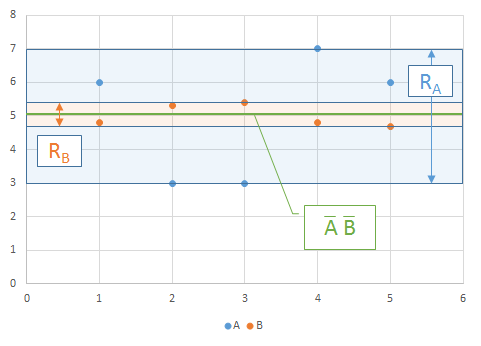
どちらも平均値は5。これをグラフにプロットしてみるとどちらがばらつきが大きいかは一目瞭然ですが、これを表す指標として標準偏差があります。
まず、個々のデータについて平均からの偏差を計算してみます。
\begin{eqnarray}
\{A_{n}-\bar{A}\}&=&+1, -2, -2, +2, +1\\
\{B_{n}-\bar{B}\}&=&-0.2, +0.3, +0.4, -0.2, -0.3
\end{eqnarray}
\{A_{n}-\bar{A}\}&=&+1, -2, -2, +2, +1\\
\{B_{n}-\bar{B}\}&=&-0.2, +0.3, +0.4, -0.2, -0.3
\end{eqnarray}
ぱっと見で偏差の大きいAのほうがばらつきは大きいことがわかるけれど、どのくらい大きいかは表現しにくいです。あたりまえだけど偏差の平均を取れば0になりますね。(偏差は平均からの乖離量だから)
符号を外してみよう(平均偏差)
平均を取って0にならないようにするには符号を外せばいい。というわけで単純に偏差の絶対値の平均を取りましょう。
\begin{eqnarray}
\frac{\sum{|A_{n}-\bar{A}|}}{n}&=&1.6\\
\frac{\sum{|B_{n}-\bar{B}|}}{n}&=&0.28
\end{eqnarray}
\frac{\sum{|A_{n}-\bar{A}|}}{n}&=&1.6\\
\frac{\sum{|B_{n}-\bar{B}|}}{n}&=&0.28
\end{eqnarray}
Aのほうがばらつきが大きいです。これが平均偏差。
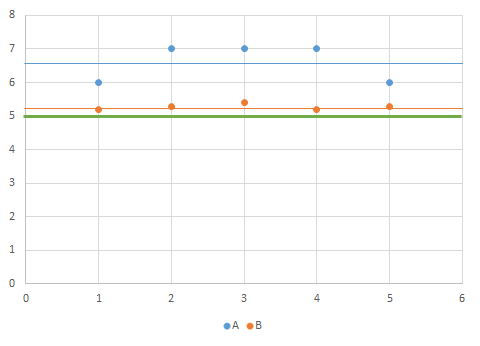
符号を外してみよう(標準偏差)
もう一つの符号の外し方が二乗して平方根を取る方法。平均偏差とはちょっと違う値が出てきます。
\begin{eqnarray}
\sqrt{\frac{\sum{|A_{n}-\bar{A}|^2}}{n}}&=&1.673\\
\sqrt{\frac{\sum{|B_{n}-\bar{B}|^2}}{n}}&=&0.289
\end{eqnarray}
\sqrt{\frac{\sum{|A_{n}-\bar{A}|^2}}{n}}&=&1.673\\
\sqrt{\frac{\sum{|B_{n}-\bar{B}|^2}}{n}}&=&0.289
\end{eqnarray}
やっぱりAのほうがばらつきが大きいですね。これが標準偏差。
ここで二乗和を取ったりその平均を取ったりしているのが、各々平方和(S)であったり分散(V)であったりします。
ただしここで計算したのは標本分散。前回出ていたのは不偏分散。数学的な違いの説明は難しいのだけれど、平均を取る際の分母がデータ数そのものの時が標本分散でデータ数-1の時が不偏分散。品質管理における統計処理では不偏分散を使用します。
不偏分散を使用して計算しなおした標準偏差は下記のようになります。データ数が少ないから結構値は変わりますね。
\begin{eqnarray}
\sqrt{\frac{\sum{|A_{n}-\bar{A}|^2}}{n-1}}&=&1.870\\
\sqrt{\frac{\sum{|B_{n}-\bar{B}|^2}}{n-1}}&=&0.324
\end{eqnarray}
\sqrt{\frac{\sum{|A_{n}-\bar{A}|^2}}{n-1}}&=&1.870\\
\sqrt{\frac{\sum{|B_{n}-\bar{B}|^2}}{n-1}}&=&0.324
\end{eqnarray}
標準偏差の桁数は有効数字3桁でいいそうです。平均値同様、こちらもJISで規定されています。