2016年秋の第7問はヒストグラム。QC七つ道具、続くねぇ。
おいちゃんは相変わらず「まず勉強してから解く」スタイルですよ。5項目を2分で解いたけど正解は3問。問題の読み違いで落としてしまった。「〜になっていないため」という問題だったので正反対の解を選んでしまったよ。もったいないね。
ヒストグラムとは
度数分布図ともいいます。計量値で表される品質特性値について、ばらつき方や平均の位置、不適合の程度などの状態を知るのに使います。
データを区間で区切ってグループとして扱い、柱状図(棒グラフ)によって分布状態の姿をつかみます。縦軸にデータの出現数(度数)を、横軸にデータの数値(特性値)を取ります。
用語
- 区間(級、クラス)
- データをある大きさで区切った間
- 区間の境界線(限界値)
- 区間同士の境目
- 区間の幅h
- 一区間の大きさ
- 区間の中心値
- 区間を代表する中心(中央)値
- 区間の数
- 柱の本数
- 度数f
- 区間の中に入るデータ数
- 分布
- データのばらつきの状態
ヒストグラムの作り方
- 特性を決める
一ヶ月で100程度となる計量値 - データを集める
データ数100以上の層別データ - データの最大値と最小値を求める
群ごとに最大値と最小値を求めて、その中からデータ全体の最大値と最小値を求めると楽 - 区間の数を決める
\(区間の数\fallingdotseq\sqrt{データ数}\)
※整数値に丸める - 区間の幅を決める
\(区間の幅h=\frac{(最大値-最小値)}{区間の数}\)
※測定のきざみ(最小測定単位の桁)に丸める - 区間の境界を決める
区間の境界値を測定のきざみ(最小測定単位の桁)の\(\frac{1}{2}\)とする
\(第1区間の下限境界値=最小値-\frac{測定のきざみ}{2}\) - 区間の中心値(x)を決める
\(区間の中心値(x)=\frac{区間の下限境界値+区間の上限境界値}{2}\) - データの度数を数えて度数表を作成する
- ヒストグラムを作成する
- 平均値(一点鎖線)や規格値(実線)を記入する
- データ数nなど検討に必要な項目を記入
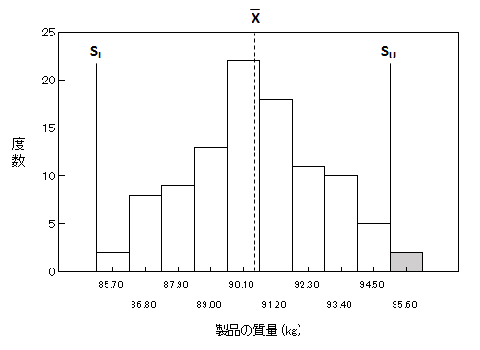
実際にやってみなくちゃわからないね。テキストのデータを使って計算して手順を確認しましたよ。
度数表から平均値と標準偏差を求める
テキストを読んでいてはるか昔に数学で習った気がしましたよ。膨大な数の生データを計算するのは大変なので(ま、今はコンピュータがあるのでそうでもないと思うけど)度数分布でざっくりまとめた値をもとに計算するものですね。当然細かい値は違ってきます。
まず謎の値uを求めておきます。数学の教科書見たら載ってんだろな。
\[u=\frac{x-x_0}{h}\]
- x:区間の中心値
- x0:仮の中心値(度数の多い中心値)
- h:区間の幅
この謎の値uと度数fを使ってufなりu2fなりを計算しておくと、ここから平均値や標準偏差を算出できます。この式自体もはるか昔に導き方を習ったんだろうな。
\begin{eqnarray}
\overline{x}&=&x_0+\frac{\sum{uf}}{n}\times{h}\\
s&=&h\times{\sqrt{\frac{1}{n-1}[\sum{u^2f}-\frac{(\sum{uf})^2}{n}]}}
\end{eqnarray}
\overline{x}&=&x_0+\frac{\sum{uf}}{n}\times{h}\\
s&=&h\times{\sqrt{\frac{1}{n-1}[\sum{u^2f}-\frac{(\sum{uf})^2}{n}]}}
\end{eqnarray}
ちなみに\(\overline{x}\)の計算式、テキストに誤植がありました。初版とはいえ数式の誤植は勘弁してほしいなぁ。